Commutative, Associative and Distributive Laws
Wow! What a mouthful of words! But the ideas are simple.
Commutative Laws
The "Commutative Laws" say we can swap numbers over and still get the same answer ...
... when we add:
a + b = b + a
a + b = b + a
Example:
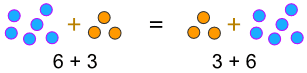
... or when we multiply:
a × b = b × a
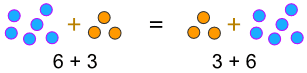
a × b = b × a
Example:
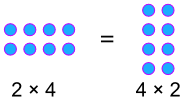
Commutative Percentages!
Because a × b = b × a it is also true that a% of b = b% of a
Example: 8% of 50 = 50% of 8, which is 4
 Why "commutative" ... ?
Because the numbers can travel back and forth like a commuter.
Why "commutative" ... ?
Because the numbers can travel back and forth like a commuter.
Associative Laws

Why "commutative" ... ?
Because the numbers can travel back and forth like a commuter.
Associative Laws
The "Associative Laws" say that it doesn't matter how we group the numbers (i.e. which we calculate first) ...
... when we add:
(a + b) + c = a + (b + c)
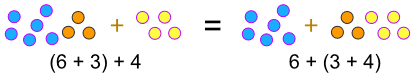 ... or when we multiply:
(a × b) × c = a × (b × c)
... or when we multiply:
(a × b) × c = a × (b × c)
(a + b) + c = a + (b + c)
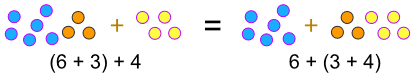
(a × b) × c = a × (b × c)
Examples:
This: (2 + 4) + 5 = 6 + 5 = 11 Has the same answer as this: 2 + (4 + 5) = 2 + 9 = 11
This: (3 × 4) × 5 = 12 × 5 = 60 Has the same answer as this: 3 × (4 × 5) = 3 × 20 = 60
| This: | (2 + 4) + 5 = 6 + 5 = 11 |
| Has the same answer as this: | 2 + (4 + 5) = 2 + 9 = 11 |
| This: | (3 × 4) × 5 = 12 × 5 = 60 |
| Has the same answer as this: | 3 × (4 × 5) = 3 × 20 = 60 |
Uses:
Sometimes it is easier to add or multiply in a different order:
What is 19 + 36 + 4?
What is 2 × 16 × 5?
Distributive Law
The "Distributive Law" is the BEST one of all, but needs careful attention.
This is what it lets us do:
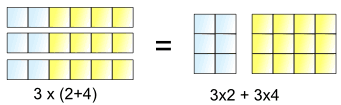 3 lots of (2+4) is the same as 3 lots of 2 plus 3 lots of 4
So, the 3× can be "distributed" across the 2+4, into 3×2 and 3×4
And we write it like this:
a × (b + c) = a × b + a × c
Try the calculations yourself:
3 lots of (2+4) is the same as 3 lots of 2 plus 3 lots of 4
So, the 3× can be "distributed" across the 2+4, into 3×2 and 3×4
And we write it like this:
a × (b + c) = a × b + a × c
Try the calculations yourself:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
Either way gets the same answer.
In English we can say:
We get the same answer when we:
- multiply a number by a group of numbers added together, or
- do each multiply separately then add them
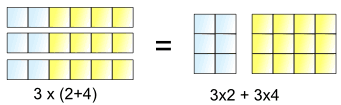
a × (b + c) = a × b + a × c
We get the same answer when we:
- multiply a number by a group of numbers added together, or
- do each multiply separately then add them
Uses:
Sometimes it is easier to break up a difficult multiplication:
Example: What is 6 × 204 ?
Or to combine:
Example: What is 16 × 6 + 16 × 4?
We can use it in subtraction too:
Example: 26×3 - 24×3
We could use it for a long list of additions, too:
Example: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
And those are the Laws . . .
. . . but don't go too far!
The Commutative Law does not work for subtraction or division:
Example:
The Associative Law does not work for subtraction or division:
Example:
The Distributive Law does not work for division:
Example:
Summary
| Commutative Laws: | a + b = b + a a × b = b × a |
| Associative Laws: | (a + b) + c = a + (b + c) (a × b) × c = a × (b × c) |
| Distributive Law: | a × (b + c) = a × b + a × c |
No comments:
Post a Comment