Laws of Exponents

Exponents are also called Powers or Indices

The exponent of a number says how many times to use the number in a multiplication.

In this example: 8² = 8 × 8 = 64

In words: 8² could be called "8 to the second power", "8 to the power 2" or simply "8 squared"

Try it yourself:

3⁴ = 3 × 3 × 3 × 3 = 81

 law of exponent

So an Exponent saves us writing out lots of multiplies!

Example: a⁷

a⁷ = a × a × a × a × a × a × a = aaaaaaa

Notice how we wrote the letters together to mean multiply? We will do that a lot here.

Example: x⁶ = xxxxxx

 

The Key to the Laws

Writing all the letters down is the key to understanding the Laws

Example: x²x³ = (xx)(xxx) = xxxxx = x⁵

Which shows that x²x³ = x⁵, but more on that later!

So, when in doubt, just remember to write down all the letters (as many as the exponent tells you to) and see if you can make sense of it.

All you need to know ...

The "Laws of Exponents" (also called "Rules of Exponents") come from three ideas:

	The exponent says how many times to use the number in a multiplication.
	A negative exponent means divide, because the opposite of multiplying is dividing
	A fractional exponent like 1/n means to take the nth root:

If you understand those, then you understand exponents!

And all the laws below are based on those ideas.

Laws of Exponents

Here are the Laws (explanations follow):

Law	Example
x1 = x	61 = 6
x0 = 1	70 = 1
x-1 = 1/x	4-1 = 1/4
xmxn = xm+n	x2x3 = x2+3 = x5
xm/xn = xm-n	x6/x2 = x6-2 = x4
(xm)n = xmn	(x2)3 = x2×3 = x6
(xy)n = xnyn	(xy)3 = x3y3
(x/y)n = xn/yn	(x/y)2 = x2 / y2
x-n = 1/xn	x-3 = 1/x3
And the law about Fractional Exponents:

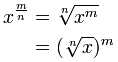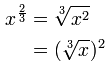Laws Explained

The first three laws above (x¹ = x, x⁰ = 1 and x^-1 = 1/x) are just part of the natural sequence of exponents. Have a look at this:

Example: Powers of 5
	.. etc..
52	1 × 5 × 5	25
51	1 × 5	5
50	1	1
5-1	1 ÷ 5	0.2
5-2	1 ÷ 5 ÷ 5	0.04
	.. etc..

Look at that table for a while ... notice that positive, zero or negative exponents are really part of the same pattern, i.e. 5 times larger (or 5 times smaller) depending on whether the exponent gets larger (or smaller).

The law that x^mxⁿ = x^m+n

With x^mxⁿ, how many times do we end up multiplying "x"? Answer: first "m" times, then by another "n" times, for a total of "m+n" times.

Example: x²x³ = (xx)(xxx) = xxxxx = x⁵

So, x²x³ = x⁽²⁺³⁾ = x⁵

The law that x^m/xⁿ = x^m-n

Like the previous example, how many times do we end up multiplying "x"? Answer: "m" times, then reduce that by "n" times (because we are dividing), for a total of "m-n" times.

Example: x⁴/x² = (xxxx) / (xx) = xx = x²

So, x⁴/x² = x^(4-2) = x²

(Remember that x/x = 1, so every time you see an x "above the line" and one "below the line" you can cancel them out.)

This law can also show you why x⁰=1 :

Example: x²/x² = x^2-2 = x⁰ =1

The law that (x^m)ⁿ = x^mn

First you multiply "m" times. Then you have to do that "n" times, for a total of m×n times.

Example: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

So (x³)⁴ = x^3×4 = x¹²

The law that (xy)ⁿ = xⁿyⁿ

To show how this one works, just think of re-arranging all the "x"s and "y"s as in this example:

Example: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

The law that (x/y)ⁿ = xⁿ/yⁿ

Similar to the previous example, just re-arrange the "x"s and "y"s

Example: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

The law that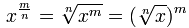 

OK, this one is a little more complicated!

I suggest you read Fractional Exponents first, or this may not make sense.

Anyway, the important idea is that:

x^1/n = The n-th Root of x

And so a fractional exponent like 4^3/2 is really saying to do a cube (3) and a square root (1/2), in any order.

Just remember from fractions that m/n = m × (1/n):

Example: 

The order does not matter, so it also works for m/n = (1/n) × m:

Example: 

Exponents of Exponents ...

What about this example?

4³²

We do the exponent at the top first, so we calculate it this way:

Start with:		432
32 = 3×3:		49
49 = 4×4×4×4×4×4×4×4×4:		262144

 

And That Is It!

If you find it hard to remember all these rules, then remember this:

you can work them out when you understand the
three ideas near the top of this page

 

Oh, One More Thing ... What if x = 0?

Positive Exponent (n>0)		0n = 0
Negative Exponent (n<0)		0-n is undefined (because dividing by 0 is undefined)
Exponent = 0		00 ... ummm ... see below!

 

The Strange Case of 0⁰

There are different arguments for the correct value of 0⁰

0⁰ could be 1, or possibly 0, so some people say it is really "indeterminate":

	x0 = 1, so ...	00 = 1
	0n = 0, so ...	00 = 0
	When in doubt ...	00 = "indeterminate"